How many halves fit into a quarter? Half of them
✅ Math is hard
❌ This math is hard
p/q=q
So q=√p
Works with a lot of numbers ☝🏻🤓
If you give half a person a quarter of a thing, how much would you be giving a full person? That’s right baby, half a thing. Don’t sweat it.
x / sqrt(x) = sqrt(x)
Damn who would’ve thought?
I just think of division as how many times the right expression fits inside the left expression. 0.5 fits into 0.25 only 0.5 aka 1/2 times, because only half of it fits.
Precisely this. The people not getting the OP are why Common Core was developed.
The numbers between zero and one are where all of the fun is!
25/5=5
2.5/0.5=5
o.O
I think, it is the real world logic that makes it hard to grasp. If you divide something with something small it becomes bigger. Mathematically it’s easy and makes sense, but it it’s somehow not intuitive. Especially for young me :)
Except that’s not what’s written.
It’s 0.25/0.5
Raising it exponentially would be
2.5/5, or
25/50=50
1/2≠50. Does not compute.
It’s going to be okay:
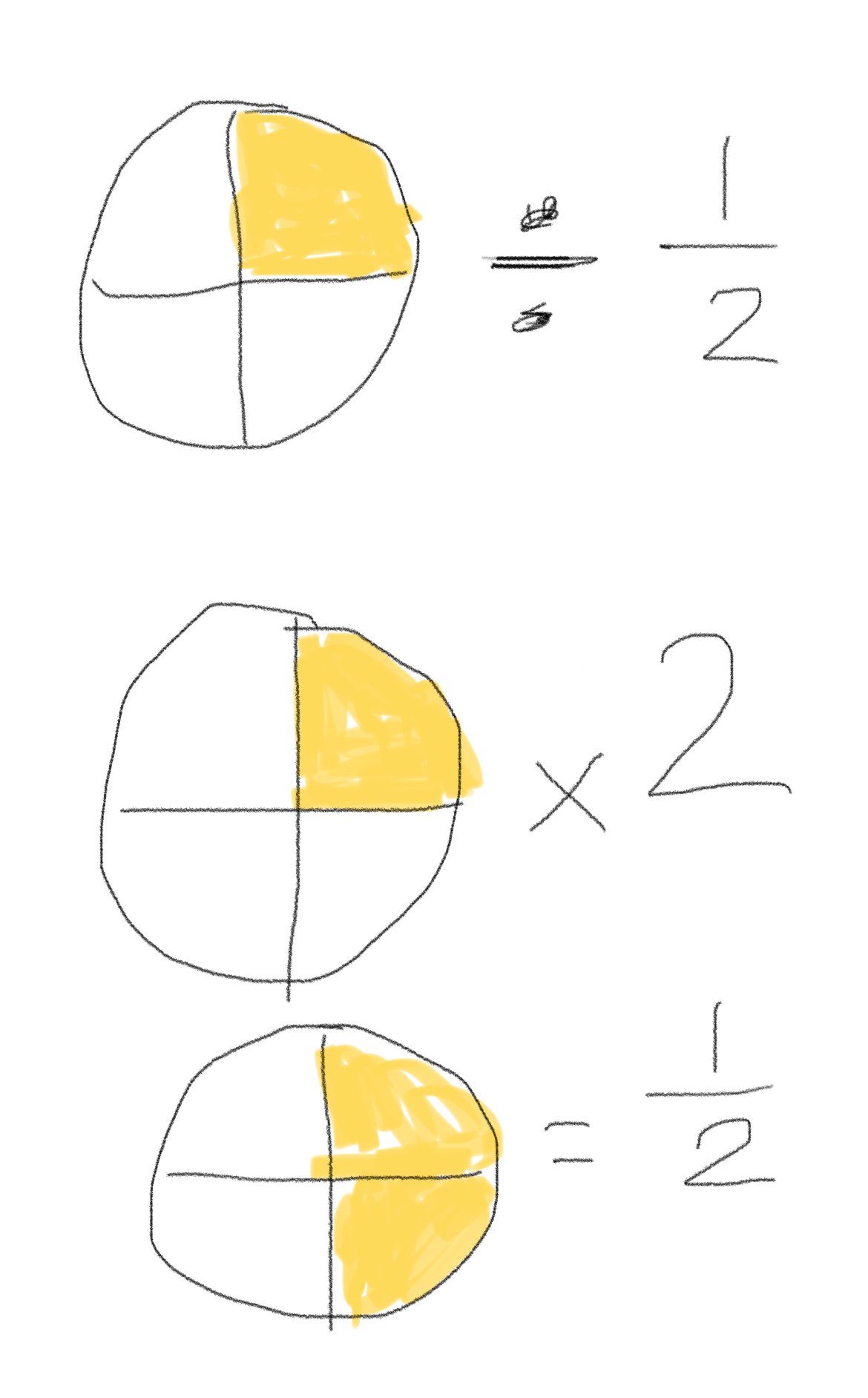
Edited to add this: Singapore math insists however, that we eliminate the use of visuals in describing arithmetic within the rationals. They encourage that users of common core rely upon the number line, and solely the number line for thorough and most mathematically sound representations of arithmetic, even when involving the division of fractions.
For those not up to speed to with common core, remember how the teacher used to draw a diagram of a bunny hopping from one integer to the next integer to represent adding given integers, such as 4+3, or -2+1? Imagine that representation being used with problems like 1/7 divided by 5/49, and no decimal approximation is allowed. It’s fascinating and truly something to appreciate from the standpoint of someone who truly loves mathematics. I think it makes for great discussions amongst math graduates like myself, and other math enthusiasts. What does that mean for those who are not so enthused? Sometimes it means the teacher receives death threats from angry students. You can’t make everyone happy.
I’m not sure I completely agree with the number-line-only approach, but I’m definitely sympathetic to it. It reinforces the idea that fractions are numbers like any other numbers, and not pieces of pizza.
I get that. I like the number line approach, and respect it, but I have also observed seasoned math coaches fumble the visual explanation of a division by fractions problem where the numerators and denominations were relatively prime. As soon as the guy had drawn the first fraction and began to say, “we’d multiply by the recipro-…”, I could tell it was going to be long problem. He just stood there, and then asked, “well, how would I go about explaining the ‘keep change flip’, if you will?” He ended the problem by saying he might just explain that the distance drawn for the first fraction needs to be repeated on the other side of the fraction to show the multiplication by the denominator of the second fraction, and then that distance could be broken into parts to demonstrate the division by the previous numerator of the second fraction.
Basically he ended the problem by saying, “let’s just reflect it! Then we can break it up.” There wasn’t really a sound justification for the reflection piece of the process, other than saying, “we need to multiply by the reciprocal of the second fraction, so we’ll just have to multiply by its denominator it had, prior to flipping it.”
That was the quietest meeting I have ever seen amongst that group of adults.
A quarter is one half of one half. Makes perfect sense.
2^-2 * (2-1)-1 = 2^-2 * 2^(-1 * -1) = 2^(-2 + -1 * -1) = 2^(-2 + 1) = 2^-1 = 1/2 = 0.5
This just comes down to the fact that “dividing by a fraction is the same as multiplying by the inverse of the fraction” is an easy rule to follow but not particularly intuitive. In natural language, when most people hear “divide by half” they’re actually picturing “divide by two” in their head.
,25/,5 x 100/100 = 25/50 = 1/2
Why was that hard?
100/100 = 1, because any number divided by itself is 1.
And any number multiplied by 1 is still that number.
TBH, I moved the decimal over 2 places on the numerator and denominator and simplified 25/50 to 1/2 because It is easier to do in my head. Some of the other paths are too complicated when I am going to sleep.
This don’t avoid to sleep not even for 1/2 second. But pick any number. If that number is even, divide it by 2. If it’s odd, multiply it by 3 and add 1. Now repeat the process with your new number. If you keep going, you’ll eventually end up at 1.
You can’t prove that!
Yes, but everyone tried since a century to find a number with which it don’t work, good to avoid sleep.
(1/4) ÷ 1/2 = 2/4 = 1/2 = 0.5








